O problema da solução ingênua da obtenção de valores aleatórios.

Considere que você quer fazer um programinha que “role” um dado de 6 faces. Geralmente, alguém faz algo assim:

int r;

srand( time( NULL ) );
r = rand() % 6 + 1;

A ideia é que obter o resto da divisão por 6 acarretará em valores menores que 6 (de 0 até 5) e somando 1, obtemos um dos 6 valores possíveis. Mas há um problema!

Considere que rand() retorna valores entre 0 e RAND_MAX que, em arquiteturas de 32 bits ou mais pode equivaler a , ou seja, o valor máximo é 2147483647 (31 bits setados). Isso representa um em 2147483648 possíveis valores e essa quantidade não é divisível por 6! Outra forma de pensar nisso é que temos 357913941 blocos de 6 valores possíveis e um bloco incompleto com os 2 primeiros valores, ou seja, no último bloco faltam 4 possibilidades para ter uma distribuição uniforme de valores possíveis.

Outra forma de pensar no assunto é essa: Considere que você tenha um dado de 6 faces e queira escolher, aleatóriamente, 1 entre 4 itens (a, b, c, d). As possibilidades são: (1=a, 2=b, 3=c, 4=d, 5=a e 6=b). Os itens a e b têm mais chance de serem escolhidos (2 chances em 6, cada) porque não temos uma distribuição de valores aleatórios uniforme! A solução é nos livrarmos dos 2 últimos valores, seja “jogando” o dado novamente, colhendo apenas um dos 4 valores possíveis, ou aplicando alguma regra maluca para nos livrarmos desses dois valores. Infelizmente, a segunda hipótese não é tão simples…

Considere agora o retorno de rand() como mostrado no fragmento de código lá em cima. Obteremos valores entre 1 e 6. Acontece que temos um espaço amostral de valores (RAND_MAX) dividido em blocos de 6 elementos, onde o último bloco só tem 2 (). Assim, a chance de obtermos 1 ou 2 são de e de obter os outros 4 valores são de . Ora . Não precisa ser um gênio para entender que 1 e 2 podem ocorrer mais vezes que os outros 4 valores.

A solução para esse problema não é trivial e, acredito, que nem mesmo seja possível num ambiente computacional binário. Em primeiro lugar, qualquer algorítmo que nos dê um valor aleatório conterá um valor entre outros. Ao obter o resto da divisão para limitar o escopo, criaremos, automaticamente, um último grupo incompleto, se o divisor não for, também, um valor menor ou igual a quantidade de amostras possíveis… Tudo o que podemos fazer é diminuir o erro relativo das distribuições e nisso rand() pode ser confiável, já que os erros relativos das distribuições, no nosso exemplo, são de, respectivamente, para 1 e 2; e para o resto:

Ou seja, a cada 500 milhões () de escolhas, aproximadamente, teremos mais 1’s e 2’s que o resto. Poderíamos melhorar esse erro de distribuição aumentando a quantidade de bits do valor aleatório. Se tivessemos 18446744073709551616 amostras (64 bits) teríamos 4 valores no último grupo e 3074457345618258603 grupos. As chances dos valores de 1 a 4 seriam de e de 5 e 6 seria de , Os erros de distribuição relativos da primeira faixa seriam de, aproximadamente, e da segunda, , ou seja, em 50 quatrilhões de “jogos” observaríamos o problema, que só se repetiria nos próximos 50 quatrilhões de jogadas, possivelmente.

Ahhh, mas eu sou um chato né? O erro é tão pequeno para aplicações práticas, não é? Acontece que RAND_MAX só tem 31 bits de tamanho em certos compiladores e certas arquiteturas. Outras podem usar valores muito menores, como 32767 (15 bits). De fato, a especificação ISO 9989 sugere que esse seja o valor mínimo para RAND_MAX, mas ele pode ser ainda menor!

Assim, neste caso, teríamos 5462 blocos e o último teria apenas 2 valores (como com 31 bits) e as distribuições seriam de (para 3 até 6) e (para 1 e 2), o que daria, para o maior erro relativo, um valor muito grande (0.012% para 1 e 2). A cada 10000 jogadas você perceberia o problema. Você já pode considerar esse dado “viciado”…

Ahhhh… note que não estou considerando que rand() geralmente é implementado usando LCG que oferece menos aleatoriedade nos bits inferiores. Assim, obter o resto de uma divisão por um valor pequeno tende a criar valores ainda menos aleatórios.

Indo a extremos para evitar usar ponto flutuante. Você deveria fazer isso também!

Eis um problema que preciso resolver para o meu mais novo projeto de brinquedo: Preciso determinar se uma imagem (stream de vídeo) tem aspecto mais próximo do aspect ratio ou do . A solução mais “simples” é simplesmente dividir o comprimento (width) pela altura (height) e comparar o resultado com uma fração de ‘meio termo”. O “meio termo”, é claro, é a média aritmética simples dos dois aspectos:

Por que a fração de “meio termo”? É que o vídeo pode ter resolução não padronizada e, neste caso, colocarei “barras pretas” horizontais ou verticais, dependendo do aspecto. Assim, temos:

int is_letterbox(unsigned int width, unsigned int height)
{
  double ratio = ( double )width / height;

  return ratio <= 14.0 / 9.0;
}

Nada mais simples, né? Se o aspecto for menor ou igual a , então encaro o vídeo como candidato para ser convertido para letterbox, ao invés de widescreen. Ahhh… sim… note que o operador de comparação (<=) tem menor precedência que o de divisão (/)… Por isso a expressão intera faz o que queremos!

O problema é que nem a divisão de , nem a divisão são exatas. Bem… a primeira até pode resultar num valor exato, mas o quociente constante de não! Isso poderia causar um “falso positivo” no caso de teste por “menor que” e um “falso negativo” no caso do teste de igualdade… Mas, aqui temos um outro problema: Imagine que o vídeo tenha resolução de 1400×901. Isso dará um aspecto de , necessariamente, que é muito próximo de .

Falei “necessariamente” porque para obter a manor fração possível podemos usar o “máximo divisor comum” para fazer a divisão do dividendo e divisor (inteiras), obtendo os menores valores. Por exemplo:

#include <stdio.h>
#include <stdlib.h>

static unsigned int gcd( unsigned int, unsigned int );

int main( int argc, char *argv[] )
{
  unsigned int w, h, d;

  if ( argc != 3 )
  {
    fputs( "ERROR\n", stderr );
    return EXIT_FAILURE;
  }

  w = atoi( argv[1] );
  h = atoi( argv[2] );

  d = gcd( w, h );

  printf( "%u/%u -> %u/%u\n",
          w, h, w / d, h / d );

  return EXIT_SUCCESS;
}

unsigned int gcd( unsigned int a, unsigned int b )
{
  unsigned int t;

  if ( a < b )
  {
    t = a;
    a = b;
    b = t;
  }

  if ( ! b )
    return 1;

  while ( b )
  {
    t = b;
    b = a % b;
    a = t;
  }

  return a;
}

Compilando e testando:

$ cc -o test test.c
$ ./test 1280 720
1280/720 -> 16/9
$ ./test 1400 901
1400/901 -> 1400/901
$ ./test 1400 920
1400/920 -> 35/23

Se formos comparar o numerador e o denominador isoladamente a coisa vai complicar um bocado. Note que mesmo numa resolução maluca diferente (1400×920) o aspecto ainda tem o dividendo e divisor bem diferentes ().

De volta ao ensino fundamental:

Como sabemos que, por exemplo, é maior que ? A solução que você aprendeu lá no ensino fundamental é converter ambas as frações ao mesmo denominador. Daí podemos comparar diretamente os numeradores, certo? Basta multiplicar ambos o numerador e o denominador de ambas as frações pelo denominador da outra fração:

Agora, com ambas as frações “normalizadas”, podemos comparar diretamente os numeradores. No caso, 10 é maior que 9 e, por isso, é maior que …

Vocẽ reparou que não precisamos mais nos preocupar com os denominadores se simplesmente multiplicarmos um numerador pelo denominador da outra fração, né? Isso facilita um bocado a nossa rotina is_letterbox(), evitando o uso de ponto flutuante:

int is_letterbox( unsigned int width, unsigned int height )
{
  unsigned int n1, n2;

  /* Não precisamos calcular os denominadores! */
  n1 = width * 9;   // 9 de 14/9
  n2 = 14 * height; // height de width/height

  return n1 <= n2;
}

Comparando as duas rotinas:

Compilando com otimizações e gerando o código em assembly:

$ cc -O2 -mtune=native -S -masm=intel test.c

Olhem só isso, com ambos os códigos lado a lado:

is_letterbox_fp:                  is_letterbox_int:      
  mov edi, edi                      imul  esi, esi, 14
  mov esi, esi                      lea eax, [rdi+rdi*8]
  pxor  xmm0, xmm0                  cmp eax, esi
  xor eax, eax                      setbe al
  pxor  xmm1, xmm1                  movzx eax, al
  cvtsi2sdq xmm0, rdi               ret
  cvtsi2sdq xmm1, rsi
  divsd xmm0, xmm1
  movsd xmm1, [rip+.LC0]
  ucomisd xmm1, xmm0
  setnb al
  ret

.LC0:
  dq 14.0 / 9.0  ; funciona no NASM.

Pra começar, a segunda rotina não tem divisões (que são LERDAS!). Ainda, a segunda rotina, além de ser menor, é melhor otimizada pelo processador (fusões, reordenações, etc). Outra vantagem é que, na primeira rotina, se height for zero, ela nos causará problemas porque a divisão resultará em NaN, que sempre retornará falso na comparação em ponto flutuante! Mais uma: A comparação, na segunda rotina, é sempre exata!

O único problema da segunda rotina poderia ser o caso de ocorrência de overflows, mas, como as resoluções gráficas que usaremos não resultam em frações com componentes muito grandes (pelo menos, não o suficiente para, quando multiplicados por 9 e 14 causem overflows), então a rotina é bem segura. Se, mesmo assim, você quer evitar a possibilidade de overflows, mude os tipos de n1 e n2 para unsigned long int ou unsigned long long. É prudente colocar um ‘UL‘ depois das constantes ou fazer um casting das variáveis nas multiplicações:

;  int is_letterbox( unsigned int width, 
;                    unsigned int height )
;  {
;    unsigned long n1, n2;
;  
;    n1 = width * 9UL;
;    n2 = 14UL * height;
;  
;    return n1 <= n2;
;  }
is_letterbox:
  mov esi, esi         ; Apenas para zeras os 32 bits
  mov edi, edi         ; superiores dos argumentos.

  lea rax, [rsi*8]     ; RAX = height*8
  lea rdx, [rdi+rdi*8] ; RDX = width*9
  sub rax, rsi         ; RAX = height*7
  add rax, rax         ; RAX = height*14

  cmp rdx, rax
  setbe al
  movzx eax, al
  ret

Mesmo assim o código ainda é melhor que o equivalente em ponto flutuante.

Siga o conselho do Tio Fred: Fuja de ponto flutuante sempre que puder.

Como NÃO tentar criar um gerador de valores aleatórios…

Já falei sobre o LCG (Linear Congruential Generator) e outros algoritmos como o Mersene Twster e o XorShift128+. Todos eles são “pseudo” geradores de valores aleatórios, já que não é possível gerar valores aleatórios com métodos determinísticos. Aliás, gerar valores aleatórios é um troço bem difícil porque a maioria dos fenômenos físicos tendem a oferecer um padrão, dada uma quantidade razoável de amostras. Por exemplo, se você jogar a mesma moeda, num jogo de “cara ou coroa”, digamos, 1 milhão de vezes, observará que a quantidade de “caras” ou “coroas” é maior que a outra. Ou seja, você pode prever, com maior segurança (embora não exatamente) qual será o resultado da próxima jogada…

De fato, até onde sei, os únicos fenômenos aleatórios são ao nível quântico (variação de fuga de carga num semnicondutor aquecido, por exemplo… Ou o decaimento radioativo num intervalo de tempo pequeno o suficiente)… De fato, também já falei por aqui, um desses fenômenos é usado, hoje em dia, para disponibilizar um DTRNG (Digital True Random Number Generator), presente dentro de todos os processadores da família Intel (pelo menos nos Ivy Bridge em diante) e acessíveis através da instrução RDRAND.

Mas, note: Mesmo que o LCG e outros métodos não criem valores verdadeiramente aleatórios, num escopo restrito e onde não há preocupação com a “aleatoriedade absoluta”, eles podem ser encacrados como geradores aleatórios reais. Abaixo, mostro um programinha que cria uma imagem de 1024×1024 pixels (RGB) com base na função rand() da biblioteca de C:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// Scale 'n' to 24 bits (0xBBGGRR).
#define rand2rgb(n) \
  ( ( int ) ( ( (n) * 16777215.0 ) / RAND_MAX ) )

int main ( void )
{
  int x, y, r;

  srand( time(NULL) );

  fputs( "P6\n1024 1024\n255\n", stdout );

  for ( y = 0; y < 1024; y++ )
    for ( x = 0; x < 1024; x++ ) 
    { 
      r = rand2rgb(rand());
      fwrite( &r, 3, 1, stdout );  // assume little endian. 
    }
}

Compilando e executando:

$ cc -O2 -o random random.c
$ ./random > rand1.ppm

Obtemos um arquivo rand1.ppm assim:

Ruído gerado por cores “aleatórias” dos pixels.

Recentemente vi alguém, num forum, tentando implementar seu próprio PRNG na rotina mcc_rnd(), abaixo:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <limits.h>

// Scale n to 24 bit value (0xBBGGRR).
// OBS: Uses long double because 'long' is 64 bits long in x86-64 systems.
#define rand2rgb(n) \
  ( ( int ) ( ( (n) * 16777215.0L ) / LONG_MAX ) )

// using size_t instead of ptrdiff_t (same thing)
typedef size_t mcc_rnd_t;

static long mcc_rnd ( mcc_rnd_t *seed, long min, long max );

int main ( void )
{
  int x, y;
  int r;
  long seed = 1;

  fputs ( "P6\n1024 1024\n255\n", stdout );

  for ( y = 0; y < 1024; y++ )
    for ( x = 0; x < 1024; x++ ) 
    { 
      r = rand2rgb ( mcc_rnd ( &seed, 0, LONG_MAX ) ); 
      fwrite ( &r, 3, 1, stdout );
    }
}

long mcc_rnd ( mcc_rnd_t *seed, long min, long max )
{
  // Most of the time tmp will point to the SAME memory block
  // for every process. Notice that, probably, tmp is aligned,
  // meaning the lower bits aren't 'random' at all... 
  // and the upper bits isn't random as well...
  void *tmp = malloc ( 1 );

  long val = time ( NULL ) + ( size_t ) tmp;

  free ( tmp );

  // This isn't 'random' seed. Taking the argument address means 
  // it will be copied to the stack and the stack pointer isn't
  // that 'random'... The value on stack isn't that unpredictable
  // as you think!
  if ( ! seed )
    seed = ( mcc_rnd_t * ) ( &seed );

  // Well... this isn't random, again, isn't it?
  if ( ! *seed )
    *seed = 1;

  val %= *seed;
  val *= clock();

  // The seed, again, isn't random!
  *seed <<= 1; 

  // Saturation get even less random values! 
  return ( val > max ) ? max : ( val < min ? min : val );
}

Os comentários na função mcc_rnd() são meus. A rotina tem várias falhas:

1. malloc() retorna um endereço no virtual address space, que tende a ser o mesmo para todos os processos;
2. Dependendo da velocidade com que a rotina é chamada, time() e clock() retornam o mesmo valor;
3. clock() não mede a quantidade de ciclos de clock do processador, mas tem uma granulidade muito maior. Mesmo que medisse, teríamos valores praticamente sequenciais;
4. A semente (*seed), usada como divisor, é tudo menos aleatória;
5. A “saturação”, no caso de valores “fora da faixa” torna a rotina não aleatória!

De fato, compilando e executando, obtemos uma imagem assim:

Além da maioria dos valores serem zero, os pixels coloridos seguem padrões específicos. Notem os muitos pixels vermelhos e os gradientes do verde para o azul nos “blocos” acima…

Bem… minha dica: Não tente inventar um PRNG na base da tentativa e erro ou assumindo que certos “fenômenos” são aleatórios…

Convertendo uma string para ponto flutuante

Não vou mostrar código aqui porque seria um bem grande e com alguns macetes e testes de condições especiais (como NaNs, overflows, underflows). Para dar uma olhada no código atual da glibc, obtenha o código-fonte (no Debian/Ubuntu: apt source libc6) e veja o arquivo stdlib/strtod_l.c.

O problema em questão aqui é como transformar uma string contendo um valor decimal que tenha componente fracionário para ponto flutuante. Para tanto, usarei o tipo float como base (porque tem menos bits significativos – me permitirá escrever menos!). Considere o valor de PI com algumas “casas decimais” de “precisão”: 3.14159

Converter a parte inteira é trivial: Basta realizar múltiplas divisões por 2 e os restos nos darão os bits à partir do MSB. Neste caso, 3 é 0b11. Mas, e quanto a parte fracionária? O motivo que dividirmos por 2 o valor inteiro até obtermos zero como quociente é que cada posição do componente inteiro é um múltiplo de 2, em binário. Ou seja, 3 é . No caso da parte fracionária, os fatores multiplicadores dos bits são da ordem de . O expoente negativo indica que o valor de cada bit deverá ser dividido pela potência de dois. A operação inversa, então, é multiplicar o valor decimal fracionário por 2 e obter o valor inteiro que, necessariamente, será 0 ou 1. No caso, . Obtivemos 0, na parte inteira, e 0.28318 na parte fracionária… Esse 0, inteiro, é o MSB da parte fracionária… No segundo passo, multiplicamos apenas a parte fracionária resultante (0.28318) por 2. A parte inteira do resultado é o próximo bit e repetimos tudo para os próximos bits (eis todos os cálculos para 25 bits):

0.14159 * 2 = 0.28318 (MSB fracionario = 0)
0.28318 * 2 = 0.56636 (0)
0.56636 * 2 = 1.13272 (1)
0.13272 * 2 = 0.26544 (0)
0.26544 * 2 = 0.53088 (0)
0.53088 * 2 = 1.06176 (1)
0.06176 * 2 = 0.12352 (0)
0.12352 * 2 = 0.24704 (0)
0.24704 * 2 = 0.49408 (0)
0.49408 * 2 = 0.98816 (0)
0.98816 * 2 = 1.97632 (1)
0.97632 * 2 = 1.95264 (1)
0.95264 * 2 = 1.90528 (1)
0.09528 * 2 = 1.81056 (1)
0.81056 * 2 = 1.62112 (1)
0.62112 * 2 = 1.24224 (1)
0.24224 * 2 = 0.48448 (0)
0.48448 * 2 = 0.96896 (0)
0.96896 * 2 = 1.93792 (1)
0.93792 * 2 = 1.87584 (1)
0.87584 * 2 = 1.75168 (1)
0.75168 * 2 = 1.50336 (1)
0.50336 * 2 = 1.00672 (1)
0.00672 * 2 = 0.01344 (0)
0.01344 * 2 = 0.02688 (0)
...

Assim o valor final de 3.14159 é, em binário, com 27 bits de precisão é 0b11.0010010000111111001111100.

Como estamos lidando com float e já temos 2 bits na parte inteira, precisamos fazer essas repetições apenas 23 vezes. Uma vez a mais para determinar se precisaremos arredondar o valor obtido. Se a precisão de um float é de 24 bits, é necessário obter 25 para usar esse bit extra para arredondamento.

Da sequência acima, obtemos o valor 0b11.00100100001111110011111. Agora, precisamos normalizar esse valor, deixando apenas 1 bit setado na parte inteira. Isso é feito deslocando o “ponto binário” 1 bit para a esquerda. O valor obtido é 0b1.10010010000111111001111_1. Como o bit inferior, além da precisão do float, ou seja, dos 23 bits da parte fracionária, é 1, arredonda-se o valor da “mantissa” (de 23 bits, em vermelho) para cima, acrescentando 1, obtendo: 0b1.10010010000111111010000.

Agora, note que, na equação que nos dá o valor contido na estrutura de um float:

O valor inteiro f nada mais é do que a parte fracionária, binária, deslocada 23 bits para a esquerda, ignorando o valor inteiro normalizado, ou seja, f é 0b100_1001_0000_1111_1101_0000 (0x490fd0 ou 4788176). Agora temos e :

Que é a representação mais próxima de 3.14159 que podemos conseguir com um float.

Neste ponto você deve estar pensando que é meio esquisito que uma rotina de conversão de string para ponto flutuante precise usar ponto flutuante. Isso é, mais ou menos, a história do ovo e da galinha (embora o “ovo” tenha surgido primeiro! A galinha evoluiu de outras espécies que botavam ovos!), mas a rotina geralmente usa aritmética de múltipla precisão e é até possível usar BCD (Binary Coded Decimal) para tanto… De novo, a rotina ____STR2F_INTERNAL() em strtod_l.c é bastante intrincada porque leva em contra aqueles underflows e overflows, mas também a notação xxx.xxx...E+/-eee, mas o princípio fundamental é esse ai em cima!

Transformando uma divisão inteira em multiplicação

É muito comum, na maioria das arquiteturas, que as instruções de divisão (quando existem) sejam bem mais lentas que as instruções de multiplicação (quando existem). Assim, é também comum que bons compiladores transformem divisões inteiras por divisores “invariantes” (constantes) em multiplicações:

O problema aqui é que resultará num valor em ponto flutuante e queremos evitar isso… Para resolver esse problema, vajamos o que acontece quanto calculamos em ponto flutuante (usando precisão simples). Lembre-se que na estrutura de um float temos precisão de 24 bits e o valor final corresponde à equação:

Vamos assumir, como exemplo, que e teremos:

Esse valor de f pode ser obtido manualmente ou através desse pequeno código:

#include <stdio.h>

struct fp_s {
  unsigned int f:23;
  int e:8;
  int s:1;
};

int main( void )
{
  float f = 1.0f / 13.0f;
  struct fp_s *p = ( struct fp_s *)&f;

  printf( "1 / 13 = %.27f = (-1)^%d * ( 1 + %u/2^23 ) * 2^%d\n",
    f, p->s, p->f, p->e - 127 );
}

Quando multiplicamos um valor por em ponto flutuante, na verdade estaremos multiplicando o valor 10324441 (ou seja: ) e depois realizamos um shift para a direita de 27 bits. O único problema aqui é que float não tem precisão suficiente para a multiplicação de valores arbitrários para , já que possui apenas 24 bits de precisão. Precisamos de 32 bits!

O GCC faz algo similar ao que fizemos acima, mas usa precisão de 32 bits (no caso de ‘int’s). O valor é, em binário, 0b0.000_1001110110001001110110001001110_110…, onde apenas os 32 bits em vermelho nos interessam… Eles são arredondados para 0b1001110110001001110110001001111, ou 1321528399, porque o bit que segue o LSB em vermelho é 1. Como se pode observar, teremos que realizar o deslocamento de 34 bits para a direita no resultado da multiplicação desses valores inteiros (31 bits da precisão “fracionária” mais os 3 bits zerados “depois da vírgula” – exatamente como no caso do float, acima). Acontece que essa multiplicação resultatá num valor de 64 bits sempre. Então, ao invés de fazer um shift de 34 bits para a direita, só precisamos obter os 32 bits superiores e os deslocarmos para a direita em 2 bits. Ou seja:

; unsigned int f( unsigned int a ) { return a / 13; }
f:
  mov  eax,edi
  mov  edx,1321528399
  mul  edx             ; edx:eax = eax * edx
  mov  eax,edx         ; Obtemos os 32 bits superiores...
  shr  eax,2           ; ...e deslocamos em 2 bits para
                       ; direita.
  ret

A “divisão” com inteiros sinalizados é similar (só leva o sinal de a em consideração!).

; int f( int a ) { return a / 13; }
f:
  mov  eax,edi
  mov  edx,1321528399

  sar  edi,1           ; EDI = -1 se 'a' < 0 ou,...
                       ; EDI = 0, se 'a' >= 0.

  imul  edx            ; edx:eax = eax * edx
  mov  eax,edx         ; Obtemos os 32 bits superiores...
  sar  eax,2           ; ...e deslocamos em 2 bits para
                       ; direita, replicando o sinal.

  sub  eax,edi         ; Precismos subtrair 1, se o valor
                       ; de 'a' for negativo.
  ret

O motivo da subtração da unidade se é que o quociente de divisão de valores positivos é , enquanto para temos .

Tenha em mente que aqui só expliquei como o compilador calcula esses valores “mágicos” ao substituir divisões com divisores invariantes por multiplicações. Se estiver interessado em toda a matemática por trás dessa “mágica”, recomendo a leitura deste paper (aqui). Cuidado que o troço é meio complicado… ;)

Wallpaper animado usando VLC no Linux

Eis uma click-bait (e uma dica) proceis… Essa dica veio do “CLI magic”, mas eu a alterei para uso do VLC.

$ cvlc "file.mkv" --no-audio --loop --aspect-ratio '16/9' \
   --drawable-xid $(xwininfo -int -name 'Desktop' | \
                    awk '/Window id:/{print $4;}')

Repare que estou usando o CVLC para não usar a interface de janela do VLC… A linha acima retira o áudio, coloca o vídeo em loop infinito e ajusta o aspect-ratio para 16/9 (Widescreen). Outra coisa que ele faz é selecionar o “canvas” onde o vídeo é apresentado. Nesse caso, a janela do DESKTOP… Resultado (click-bait!):

É só colocar isso num script de inicialização e, voilà! :)

É conveniente que o vídeo esteja no mesmo aspect-ratio da tela, mesmo que tentemos forçar a barra para ajustar isso com a opção –aspect-ratio, o VLC tende a fazer um resize que não pode ficar muito agradável…

PS: Ainda tyem algumas coisas por fazer. Por exemplo, impedir que o título do arquivo seja mostrado por alguns segundos no início (adicione a opção --no-video-title-show); Zerar (colocar tudo preto) o fundo, caso o seu fundo não seja preto. Fundo não-preto causa blending do vídeo com o fundo, alterando as cores (não me preocupai em achar isso nas opções do VLC, ainda)… Deixo esses detalhes proceis.

Ponto fixo para ponto flutuante…

Num outro artigo (este aqui) mostrei como obter o valor representado pela estrutura de um tipo ponto flutuante (float) e vice-versa, mas não mostrei um código fonte de exemplo. Eis aqui um, mas com falhas, porque não leva em consideração valores muito grandes, muito pequenos, subnormais, infinitos e NaNs. Ele converte um valor em ponto fixo (limitado), onde a parte inteira i e a parte fracionária f do valor é fornecida à função. Como está a parte fracionária jamais poderia ser 0.01 ou 0.00034, etc. Apenas valores como: 3.14, 100.4003, etc podem ser fornecidos.

A rotina converte o valor f na componente fracionária e junta as duas numa grande variável de 64 bits, deslocando os bits até isolar o bit de mais alta ordem no bit 32 (o 1.0. implícito num float) e daí obtemos o valor em ponto flutuante. Deixo o código para a análise de vocês:

#include <stdio.h>
#include <assert.h>

// União com a estrutura de um float, para faciliar
// as coisas...
union fp_u {
  float f;

  struct {
    unsigned int m:23;
    unsigned int e:8;
    unsigned int s:1;
  } __attribute__((packed));
};

// Calcula o log, na base 10, de x.
static int log10_( unsigned int x )
{
  int n = 0;

  while ( x >= 10 )
  {
    x /= 10;
    n++;
  }

  return n;
}

// Calcula 10^x (x precisa ser menor que 10).
static unsigned long long pow10_( unsigned int x )
{
  unsigned long long n = 1;

  assert( x < 10 );

  while ( x-- )
    n *= 10;

  return n;
}

// Converte um ponto fixo no formato (i,f) para float.
// Essa rotina tem multiplas falhas:
//  A parte fracionária não permite valores como 0.01, por exemplo.
//  Não verifico por subnormais, nans e infinitos.
//  Não trato valores negativos.
float fixed2float( unsigned int i, unsigned int f )
{
  unsigned int m;
  unsigned long long n;
  int e = 0;
  union fp_u fp = { .f = 0.0 }; // OK... 0.0f é apenas 0x00000000.

  // 0.0 é um caso especial.
  if ( i != 0 && f != 0 )
  {
    // Precisamos transformat a parte fracionária na represetação binária
    // do número fixo. Poderíamos fazer isso com ponto fluautuante, mas o objetivo
    // aqui é evitar ponto flutuante, não é?
    //
    // A mágica aqui é que na representação de número fixo (iiii.ffff) a parte fracionária
    // é (f / 2³²), mas temos apenas f inteiro. Então, coloco f na parte inteira (multiplicando por
    // 2³², e divido pela grandeza do valor (10^(log(f)+1)).
    //
    // Isso garante que m terá apeans 32 bits de tamanho final e todo o cálculo é inteiro (nada de
    // ponto flutuante aqui).
    m = ( ( unsigned long long )f << 32 ) / ( pow10_( log10_( f ) + 1 ) );

    // Agora que temos a representação fracionária correta, basta colocar os dois valores
    // nas posições corretas. A parte inteira são os 32 bits superiores, a parte fracionária, os
    // 32 bits inferiores.
    n = m + ( ( unsigned long long )i << 32 );

    // Um float normalizado sempre tem 1 implícito. Assim, se qualquer um dos 31 bits supeiores for 1, 
    // então temos que fazer deslocamentos para a direita, senão, para a esquerda, até que os 32 bits
    // superiores contenha apenas 1.
    //
    // OBS: ~0ULL << 33 == 0xfffffffe00000000ULL,
    //      ~0ULL << 32 == 0xffffffff00000000ULL e, é claro,
    //       1ULL << 32 = 0x0000000100000000ULL.
    if ( n & ( ~0ULL << 33 ) )
    {
      // Ao deslocar para a direita, incrementa o expoente.
      // OBS: Dá pra melhorar isso contanto a quantidade de 'leading zeros' e deslocando a
      //      quantidade necessária de uma vez só...
      while ( ( n & ( ~0ULL << 32 ) ) != ( 1ULL << 32 ) )
      {
        n >>= 1;
        e++;
      }
    }
    else
    {
      // Ao descolar para a esquerda, decrementa o expoente.
      // OBS: Dá pra melhorar isso contanto a quantidade de 'leading zeros' e deslocando a
      //      quantidade necessária de uma vez só...
      while ( ! ( n & ( 1ULL << 32 ) ) )
      {
        n <<= 1;
        e--;
      }
    }

    fp.m = n >> 9;  // Joga fora os 9 bits inferiores (precisams de apenas 23 bits).
    fp.e = 127+e;   // Calcula o expoente do float.
    fp.s = 0; // não lido com sinal, por enquanto!

    // Acerta o arredondamento. Precisamos arredondar a "mantissa" se o 9º bit for 1.
    if ( n & 0x100 )
      fp.m++;

    // Se a "mantissa" chegou a zero, temos que delocar mais um bit, decrementando o expoente.
    if ( ! fp.m )
      fp.e--;
  }

  return fp.f;
}

// Um pequeno teste.
int main( void )
{
  printf( "%.20f = %.20f\n", 3.1416f, fixed2float( 3, 1416 ) );
}

Compilando e rodando:

$ cc -o test test.c
$ ./test
3.14159989356994628906 = 3.14159989356994628906

.

Cygwin: Gravação remota de DVD+RW

Parece (e é) estranho, alguém querer gravar DVDs nesse mundo “cloudeado”. A questão me ocorreu pois tenho um monte de dvd+rw parados que iriam pro lixo.

Pendrives são bem baratos e HDs SSDs também, mas acho que é justamente isso o que me atraiu: os CDs, DVD, Blu-rays são mídias “estáticas” e chatas de gravar, portanto ao fazê-lo, a disciplina surge automaticamente: você deve pensar no que vai colocar ali, pois irá ficar “pra sempre”.

Aquela tentação imediata de apagar a mídia é mais branda, diferente da nossa abordagem com pendrives que são “limpos” na hora, só porque você deve mandar algo para alguém. E até porque “alguém” já nem deve ter mais um leitor de dvd instalado no computador… Se ainda houver um computador!

Mas, em geral, como o que faço é para meu próprio uso, me veio então a idéia (não muito original, sei): gravar dvds usando scripts e ferramentas de linha de comando com a seguinte condição:

• Fazer isso no windows, porém através do Cygwin (nem pensar em .bat e nem naquela porcaria de powershell)

Levantei o set de comandos necessários e instalei:

• wodim
• cdrecord (front end para o wodim)
• genisoimage

Notando que o Cygwin não possui, em seu conjunto de pacotes nativos, cdrtools nem dvd+rw-tools, entendi, pela necessidade, que sendo as minhas mídias – dvd+rw – precisariam ser “formatadas” antes de gravar.

Eis os passos, após instalados os pacotes acima citados, no Cygwin (ou Linux):

1. Criar a imagem
2. Criar um checksum da imagem (se for transferir)
3. Inserir o dvd
4. Gravar usando o … dd, ao invés do wodim ou cdrecord
5. Ejetar a mídia

Mifu…

Sabem aqueles grupos onde o pessoal costuma fazer perguntas de “problemas” de cursos de graduação de computação? Do tipo “faça um programa que some 5 números…”? Well… Eu acho isso enfadonho! Mas, recentemente, topei com um que, onde “me fudi” com uma resposta irônica de minha parte (e peço desculpas, porque a solução é mesmo interessante para o aprendiz!)…

O problema era esse ai mesmo que citei acima:

“Faça um programa que leia 5 valores inteiros e apresente a soma desses valores usando apenas uma variável“

A parte em negrito é a que torna o problema interessante… Normalmente o estudante usa uma variável para ler os valores e outra para acumulá-los:

/* test1.c */
#include <stdio.h>

void main ( void )
{
  int sum, n;

  scanf ( "%d", &sum );
  scanf ( "%d", &n ); sum += n;
  scanf ( "%d", &n ); sum += n;
  scanf ( "%d", &n ); sum += n;
  scanf ( "%d", &n ); sum += n;}

  printf( "%d\n", sum );
}

Claro, isso usa duas variáveis, o que invalida a solução. Poderíamos usar um array:

/* test2.c */
#include <stdio.h>

void main ( void )
{
  int n[2];

  scanf ( "%d", &n[0] );
  scanf ( "%d", &n[1] ); n[0] += n[1];
  scanf ( "%d", &n[1] ); n[0] += n[1];
  scanf ( "%d", &n[1] ); n[0] += n[1];
  scanf ( "%d", &n[1] ); n[0] += n[1];

  printf( "%d\n", n[0] );
}

O programa acima é, essencialmente, a mesma coisa que o anterior e o estudante pode pensar que está usando apenas uma “variável”. No entanto, um arry é uma “sequência” de variáveis (a tradução direta da palavra “array” significa “sequência”), ou seja, está usando duas variáveis. Isso invalida a parte “usar apenas uma variável” do problema. Eis a solução engenhosa:

/* test3.c */
#include <stdio.h>

void main ( void )
{
  long long n;  // n tem 64 bits de tamanho!

  scanf ( "%d", ( int * )&n );

  scanf ( "%d", ( int *)&n + 1 ); 
  *( int * )&n += *( int * )(&n + 1);

  scanf ( "%d", ( int *)&n + 1 ); 
  *( int * )&n += *( int * )(&n + 1);

  scanf ( "%d", ( int *)&n + 1 ); 
  *( int * )&n += *( int * )(&n + 1);

  scanf ( "%d", ( int *)&n + 1 ); 
  *( int * )&n += *( int * )(&n + 1);

  printf( "%d\n", *( int * )&n );
}

Ao fazer o casting ( int * ) usamos a aritmética de ponteiros envolvendo o tipo int, que tem 32 bits de tamanho. Assim, ( int * )&n + 1 é uma expressão que é resolvida para os 32 bits superiores de n, enquanto ( int * )&n aponta para os 32 bits inferiores. Ao derreferenciar esse ponteiro, acessamos o seu valor, na pilha.

Em essência, estamos mexendo com um array, mas usando apenas uma variável!!! Isso atende a ambas os requisitos do problema, mas causa um problema de performance… Quando declaramos uma variável local qualquer o compilador, se tiver sido chamado com opções de otimização, tenta usar os registradores da CPU ao invés da pilha. Ao usar o operador & (endereço-de) forçamos o compilador a manter a variável na pilha. Como os scanf precisam do endereço da variável lida, os três programas, acima, geral praticamente o mesmíssimo código… Assim, cada chamda a scanf e cada acumulação usará um ou mais acessos à memória que, mesmo estando no cache L1d, poderá adicionar 1 ciclo de clock adicional às instruções (resolução do endereço efetivo).

A rotina abaixo, mais tradicional, tem o potencial de ser bem mais rápida e gastar menos espaço no cache L1i:

/* test4.c 
   Compile com: 
     gcc -O2 -fno-stack-protector -w -o test4 test4.c 
*/
#include <stdio.h>

void main ( void )
{
  int sum, n, count;

  count = 5;
  sum = 0;
  while (count--)
  {
    scanf ( "%d", &n );
    sum += n;
  }

  printf( "%d\n", sum );
}

Posso mostrar que count e sum não são mantidos na memória, mas em registradores. Apenas n não é otimizado dessa forma por causa do operador &:

; test4.asm - equivale a test4.c.
bits 64
section .rodata
scanf_fmt:  db `%d`
printf_fmt: db `%d\n`

section .text
global main
main:
  push rbp
  push rbx

  xor  ebp,ebp  ; sum=0
  mov  ebx,5    ; count=5

  sub  rsp,24   ; reserva espaço na pilha, alinhando-a

.loop:
  lea  rsi,[rsp+12]  ; n está alocado na pilha em rsp+12.
  xor  eax,eax       ; scanf() precisa disso (porquê?)
                     ; EAX, aqui, NÃO é stdin!
  mov  edi,scanf_fmt
  call __isoc99_scanf

  add  ebp,[rsp+12]  ; sum += n;
  sub  ebx,1         ; --count;
  jne  .loop         ; if (count != 0) goto loop.

  mov  edx,ebp
  mov  esi,printf_fmt
  mov  edi,1         ; stdout
  xor  eax,eax       ; printf() precisa disso (porquê?)
  call __printf_chk

  add  rsp,24   ; dealoca espaço previamente alocado na pilha.

  pop  rbx
  pop  rbp
  ret

Se não fosse pela necessidade do scanf, n também seria mantido em um registrador (R12D, por exemplo). Mas, note que temos apenas UM acesso à memória por iteração do loop (em add ebp,[rsp+12], mas, é claro, scanf também acessa memória!). No caso de test3.c temos 9 indireções, além das causadas pelo scanf, no caso de test4.c, 5.

Ahhh… lea rsi,[rsp+12] não é uma indireção, mas somente o cálculo do endereço efetivo…

Embora o exercício seja interessante, não passa de curiosidade acadêmica…

O bom, o mal e o feio

Neste artigo vou tentar mostrar 3 coisas: O algoritmo mais óbvio raramente é o melhor possível, um bom algoritmo pode ser sempre melhorado e que essa melhoria nem sempre vem sem custos. A ideia é usar um algoritmo custoso, em termos de processamento e, para isso, aqui vão os famosos testes para determinação se um valor inteiro positivo é ou não um número primo.

Nesses testes usarei o tipo unsigned int porque ele tem 32 bits de tamanho em ambas as plataformas Linux (e na SysV ABI) e Windows, tanto para o modo de operação do processador, x86-64 e i386. É bom reparar nisso, porque a determinação desse tipo de parentesco (se é primo!) em valores inteiros com mais bits pode ser muito demorada. Por exemplo, quando lidamos com o esquema de criptografia assimétrica, é comum o uso de chaves de 2048 bits de tamanho, o que torna uma das otimizações inviável (veremos adiante).

O feio

O algoritmo clássico é varrer toda a faixa de valores menores que o valor sob teste e verificar se existe algum divisor exato. Algo assim:

// Método tradicional: Tenta dividir todos os valores 
// inferiores a 'n' e conta quantos o dividem...
NOINLINE
int ugly_is_prime ( unsigned int n )
{
  unsigned int count, i;

  // caso especial.
  if ( !n ) 
    return 0;

  count = 1;
  for ( i = 2; i < n; i++ )
    if ( ! ( n % i ) )
      count++;

  return (count == 1);
}

Por que chamei essa rotina de “o feio”? Ela testa por todos os valores inferiores a n, começando por 2, se n for diferente de zero! Suponha que . Esse valor é primo, mas para a rotina determinar isso terá que percorrer todos os valores entre 2 e 4294967290. Veremos que, para isso, a rotina gasta cerca de 47 bilhões de ciclos de clock!

O mau

É claro que não precisamos verificar todos os valores! Por exemplo, 2 é o único valor par que também é primo. De cara podemos testar se n é par e diferente de 2. Se for, com certeza não é primo. Isso nos deixa os valores ímpares para teste, o que diminui pela metade o esforço computacional.

Outra melhoria que podemos fazer é a de que, de acordo com o Princípio fundamental da aritmética, todo número pode ser fatorado em números primos… Por exemplo, , , e assim por diante (voltaremos a isso no algoritmo “bom”). Ainda, “lembre-se que a ordem dos fatores não altera o produto”. Tome 10 como exemplo… Ele pode ser escrito como .

Não é evidente, mas graças a isso só precisamos testar por divisores ímpares menores ou iguais a raiz quadrada de n:

// Método "ruim" (mas, melhor que o acima).
// Faz a mesma coisa, mas só verifica os valores inferiores a 'n' 
// que sejam ímpares e menores ou iquais a raiz quadrada de 'n'.
int bad_is_prime ( unsigned int n )
{
  unsigned int sr;
  unsigned int i;

  // casos especiais.
  switch ( n )
  {
    case 1:
    case 2:
      return 1;
  };

  // O único par primo é 2.
  if ( ! ( n & 1 ) )
    return 0;

  // Obtém o valor ímpar menor ou igual
  // à raíz quadrada de n.
  sr = sqrt(n);
  if ( ! ( sr & 1 ) ) 
    sr--;

  // Só precisamos testar os valores ímpares
  for ( i = 3; i <= sr; i += 2 )
    if ( ! ( n % i ) )
      return 0;

  return 1;
}

Aqui tomo um atalho para os 2 primeiros primos (1 e 2) para simplificar a rotina.

Mas, porque essa rotina é má? O problema aqui é que, mesmo eliminando testes, estamos testando muitos valores mais de uma vez… Por exemplo, se n não for divisível por 3 ele também não será para nenhum múltiplo de 3, como 9, 12, 15, 18, 21, 24, 27… No entanto, estamos testando esses valores também, se n for grande!

O bom

A solução, é claro, é eliminar todos os valores múltiplos dos anteriores, ou seja, usar apenas divisores primos. O problema é óbvio: Ora, bolas! Como é que eu vou fazer uma rotina que testa se um valor é primo usando como critério o teste se um divisor também o é?!

O método de Erastótenes (276 AEC ~ 194 AEC) mantém uma sequência onde marcamos os valores primos, percorrendo a lista do início ao fim, e verificando se os próximos valores são múltiplos. Se forem, marcamos como “não primo”. Na próxima interação, o próximo valor é, com certeza, primo e repetimos o processo, até que todo o array contenha apenas os primos “não marcados”. Isso exige que toda a faixa de valores seja colocada no array, mas os valores usados como base de testes podem ser limitados à valores menores ou iguais a raíz quadrada de n, como fizemos anteriormente.

O ponto negativo desse método, é claro, é o consumo excessivo de memória para conter todo o array, mas, e se mantivéssemos apenas um array com os valores primos ímpares inferiores ou iguais à raiz quadrada da faixa do tipo unsigned int? Isso não consumirá tanta memória quanto você pode imaginar: Em primeiro lugar, no pior caso, teríamos um array com itens. Se cada item tem 4 bytes de tamanho, aproximadamente 128 KiB serão usados para o array. No caso mais prático, vários valores desses 32767 são eliminados, porque não serão primos.

O programinha abaixo, que usa o bad_is_prime(), acima, monta esse array:

// gentable.c
//
// Cria tabela contendo os inteiros, primos, menores ou iguais ao
// valor ímpar mais pŕoximo (porém menor) que a raiz quadrada de 2³²-1.
//
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

extern int bad_is_prime ( unsigned int );

#define ITEMS_PER_LINE 16

void main ( int argc, char *argv[] )
{
  FILE *f;
  unsigned int i, sr;
  unsigned int count = 0, cnt2 = 0;

  if ( ! *++argv )
  {
    fputs ( "Usage: gentable <cfile>\n", stderr );
    exit ( 1 );
  }

  if ( ! ( f = fopen ( *argv, "wt" ) ) )
  {
    fprintf ( stderr, 
              "ERROR opening file %s for writing.\n", 
              *argv );
    exit ( 1 );
  }

  fputs ( "// *** criado por gentable.c ***\n\n"
          "// tabela começa de 3...\n"
          "const unsigned int primes_table[] = {\n", f );

  // ~0U é o máximo valor de unsigned int.
  // Obtém a raiz quadrada ímpar...
  sr = sqrt(~0U);
  if (!(sr & 1)) 
    sr--;

  // Só precisamos dos inteiros ímpares e primos.
  for ( i = 3; i <= sr; i += 2 )
    if ( bad_is_prime ( i ) )
    {
      if ( count ) 
      {
        fputc( ',', f );

        if (++cnt2 == ITEMS_PER_LINE)
        {
          fputc ( '\n', f );
          cnt2 = 0;
        }
        else
          fputc ( ' ', f );
      }

      fprintf ( f, "%uU", i );
      count++;
    }

  fprintf ( f, "\n};\n\n"
            "// tabela ocupa %zu bytes.\n"
            "const unsigned int primes_table_items = %u;\n",
            sizeof ( unsigned int ) * count, 
            count );

  fclose ( f );
}

Basta compilar e executar o programinha para gerar um arquivo texto contendo o código fonte de uma tabela com apenas as raízes quadradas desejadas! No caso, gerarei table.c que, como pode ser observado, contém 6541 valores, ocupando apenas 25.5 KiB:

// *** criado por gentable.c ***

// tabela começa de 3...
const unsigned int primes_table[] = {
3U, 5U, 7U, 11U, 13U, 17U, 19U, 23U,
29U, 31U, 37U, 41U, 43U, 47U, 53U, 59U, 
61U, 67U, 71U, 73U, 79U, 83U, 89U, 97U,
...
... 65447U, 65449U, 65479U, 65497U, 65519U, 65521U
}; 

// tabela ocupa 26164 bytes.
const unsigned int primes_table_items = 6541;

Para essa tabela de raízes o processamento é rápido. Considere o caso de valores de 64 bits. A máxima raiz quadrada é 4294967295. Como verificar se um valor é primo é relativamente lento, pré-calcular toda a tabela pode demorar um bocado… Existe ainda o fator espaço, que explico abaixo.

Usando essa tabela, a nossa rotina de teste good_is_prime fica assim:

extern const unsigned int primes_table[];
extern const unsigned int primes_table_items;

// Método "melhor": Faz quase a mesma coisa que acima, mas
// usa uma tabela pré calculada.
int good_is_prime ( unsigned int n )
{
  unsigned int i, sr, *p;

  switch ( n )
  {
    case 1:
    case 2:
      return 1;
  }

  if ( ! ( n & 1 ) )
    return 0;

  sr = sqrt(n);

  for ( i = 0, p = (unsigned int *)primes_table; 
        i < primes_table_items && *p <= sr; 
        i++, p++ )
  {
    if ( ! ( n % *p ) )
      return 0;
  }

  return 1;
}

Ela é bem parecida com bad_is_prime, mas usa uma tabela contendo apenas valores primos para os testes!

Nem sempre usar tabelas pré-calculadas é uma boa ideia

Em primeiro lugar, poderíamos usar uma tabela pré-calculada com todos os valores primos na faixa e a rotina final poderia ser uma simples busca binária, daí a performance da rotina seria proporcional a , mas é claro que a tabela final seria enorme. Daí, escolhi armazenar apenas os valores que serão usados para verificar o divisor, eliminando os múltiplos…

A quantidade de valores primos, dado um valor máximo, pode ser aproximado (de longe!) por:

Assim, se quisermos montar uma tabela com todos os primos inferiores ou iguais à raiz quadrada do maior valor possível para um tipo, como no exemplo de unsigned int (que assume o valor máximo de 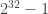), temos que o maior valor para a tabela é e, portanto, usando a aproximação acima, teríamos uma tabela com cerca de 17171 itens. Cada item cabe em 2 bytes (unsigned short), já que . O que nos daria um array de, no máximo, 33.5 KiB. Se usarmos unsigned int (como fiz) o array estimado ficaria com 67 KiB.

Observe o contraste com o que encontramos através de gentable.c… Temos menos da metade dessa quantidade! Mas isso não é garantido! Temos que assumir que a aproximação acima é uma quantidade média e usarmos como critério para estimar o custo da rotina.

Considere agora, 64 bits. Usando o mesmo critério, , que cabe num unsigned int. Daí itens com 4 bytes cada, ou seja, quase 2 GiB de array. Repare que dobramos o número de bits da faixa sob teste, mas o tamanho da tabela aumentou quase de 29 mil vezes.

Isso é esperado porque a estimativa é exponencial (proporcional a )… Então, não recomendo o método good_is_prime para valores com mais de 32 bits.

O quão bom é o “bom”?

No pior caso bad_is_prime é 10 milhões de vezes mais rápida que ugly_is_prime e good_is_prime é quase 4 vezes mais rápida que bad_is_prime (o que faz dela quase 40 milhões de vezes mais rápida que ugle_is_prime).

Estou informando esses valores, mas os medi, usando meu “contador de ciclos do homem pobre” em alguns casos:

• Melhor caso: Um valor não primo pequeno;
• Pior caso: Um valor primo muito grande: 4294967291
• Um valor não primo grande cujos fatores sejam primos grandes: 144795733, por exemplo, pode ser fatorado em 12343 e 11731.

Em alguns casos, no “melhor caso” e somente às vezes, bad_is_prime ganha de good_is_prime, mas isso ocorre, provavelmente, por causa dos efeitos do cache L1 (que só tem 32 KiB!). Isso, talvez, possa ser compensado fazendo um prefetch da tabela antes de executar a rotina… Esse é especialmente o problema quando o valor não é primo! Quando a rotina precisa varrer grande parte do o array os efeitos do cache L1 entram em ação e ela fica um pouco mais lenta que a “má” rotina…